第21回　確率はホントに収束するのか

１．はじめに

パチンコ店の経営が成り立つ以上、トータルでは店の勝ち、客の負けとなることは目に見えています。一方で、客でありながらパチンコで生計を立てている人がいます。さらには、そういういわゆるパチプロがいるにも関わらず、やはり店は利益をあげることができます。確率まかせのはずなのにどういうことなのでしょうか。

店が安定して勝てるのには理由があり、それと同じ理由でパチプロも存在できるのです。

もう、お判りと思いますが、店の経営が成り立つのは「確率が収束する」からです。もちろん不正を行う店もあるでしょう（そして不正を行うパチプロも）。しかしそれはごく一部です。「確率の収束」をきちんと理解して、稼働率を上げるなどの企業努力をしていれば、法を犯すリスクを負わなくとも経営は安定するし、同様にパチプロも生活できるのです。
（逆に言えば、稼働率を上げられない店が最終手段として遠隔操作などの不正に走るのでしょう）

２．もう少しパチンコのハナシ

収束のしくみの前に、もう少しパチンコについて説明しておきましょう。
ハナシを単純にするために、

ツいている＝理論上の大当たり頻度よりも多く当たる状態

としましょう。一ヶ月間ツいている人もいれば、フツーの状態の人もいるでしょう。しかし店はそういう全ての人のツキの平均が理論的な大当たり回数をある程度超えていても、充分収益が出るように釘を調整すれば良いわけです。

大当たり確率○○○分の１のパチンコは、その確率のくじ引きを延々と続けるゲームです。
くじを引くにはある決められた箇所に玉が入らなければなりません。10個打って１個入るのか、17個で１個なのか．．．それらをコントロールしているのが「釘」です。つまり釘はくじの単価を決めているようなモノです。
多少ツいていても釘が厳しければ（くじの単価が高いことになるので）なかなか勝てません。そうです。多少のツキなら店が勝つように釘は調整されているわけです。

一方で、あまりに釘を厳しくすると負ける人（あるいはその負け額）が増え客足が遠のいてしまうので、利益を確保しつつもある程度は甘くせざるを得ません。
つまり、まともな店なら釘の甘い台は存在し、そして甘い台を選んで（長期間継続して）打つことのできるパチプロもまた勝てるのです。

３．二項分布

例：大当たり確率1/4、くじを引く回数４回

というくじ引きを考えてみましょう。この場合、当たる回数は０回〜４回までの５通りです。それぞれが起こる確率は、

大当たり回数	計算式	結果	式の意味
０	(3/4)4	81/256	4回すべてハズレ
１	4×(1/4)×(3/4)3	108/256	１回アタリで３回ハズレ。どのひとつがアタリかが４通りある
２	6×(1/4)2×(3/4)2	54/256	２回アタリで２回ハズレ。どの２つがアタリかが６通りある
３	4×(1/4)3×(3/4)	12/256	３回アタリで１回ハズレ。どの３つがアタリかが４通りある
４	(1/4)4	1/256	４回すべてアタリ
計		256/256

ここで示した計算式は大当たり回数をｎとして一般形で書けば、

\[ {}_4 C _n \times \biggl(\frac{1}{4}\biggr)^{n} \times \biggl(\frac{3}{4}\biggr)^{4-n}　　・・・式Ａ\\ \]

となります。アタリ（確率1/4）がｎ回、ハズレ（確率3/4）が4-n回、何回目にアタリがあるかなどの組合せが4Cn通り、なのでそれぞれをかけた形になっています。
ところで、表の「計」を見てもらえればわかるとおり、この確率の合計は「１」になります。起こりうる全ての確率の合計が「１」になることに疑問はないと思いますが、もう少し説明してみましょう。

\[ (x+y)^2=x^2+2xy+y^2\\ \]

これは(ｘ＋ｙ)²を展開しただけですが、この式をバカ丁寧に書き換えると、

\[ (x+y)^2={}_2 C _0 \times x^2 \times y^0 + {}_2 C _1 \times x^1 \times y^1 + {}_2 C _2 \times x^0 \times y^2\\ \]

となります。そしてこの式の各項の一般形は、

\[ {}_2 C _n \times x^n \times y^{2-n}\\ \]

です。
式Ａと似ていますね。それもそのはず、式Ａは、

\[ (x+y)^4　　　\biggl(x=\frac{1}{4},　y=\frac{3}{4}\biggr)\\ \]

を展開したときの各項の一般形であり、先の表は展開した各項を個別に計算し合計を求めたモノなのです。ｘ＋ｙ＝1/4＋3/4＝１ですから、その合計が「１」になるのは当たり前ですね。

この様に２つの項の和（ｘ＋ｙ、あるいは1/4＋3/4）の累乗を展開する事を「二項展開」といいます。

さて、先の表をグラフにしてみましょう。

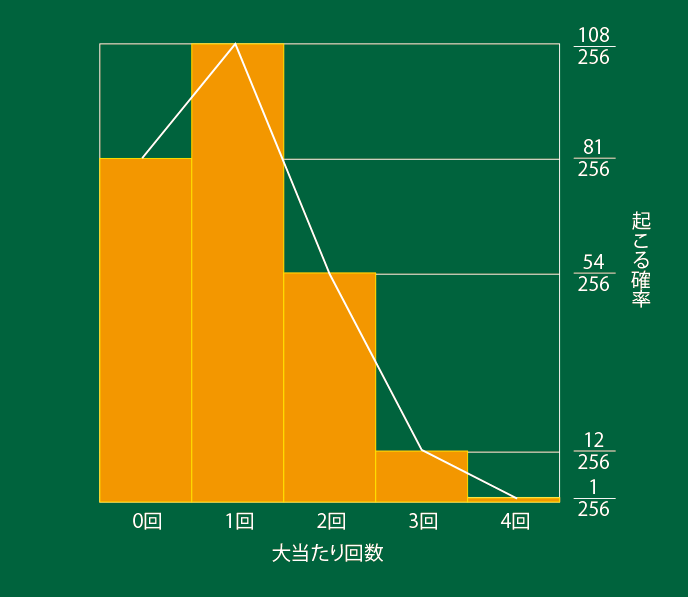
このように起こりうるケース毎の確率（をグラフにしたもの）を「確率分布」といいます。今回の場合の様に、ある確率（ここでは1/4）で起こる事象（当たり）に対して、複数回の試行で何回起こるかを表したモノを特に「二項分布」と言います。

４．二項分布から正規分布へ

くじ引きの確率分布は二項分布になることがわかりました。ゴールまでもう少しです。例では試行回数４回でしたが、もっと増やしていくとグラフはどうなっていくでしょうか。

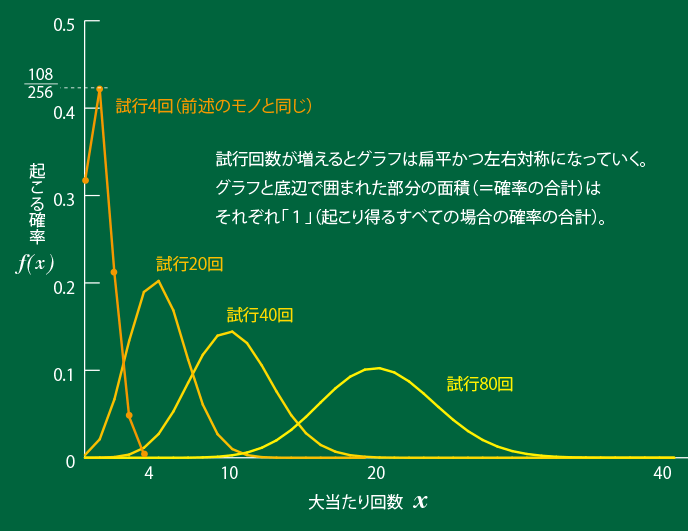
何だか確率分布らしくなってきましたね（笑）　いびつだった形が試行回数を増やすことで左右対称で滑らかなグラフになってきました。「二項分布」は試行回数が充分多ければ「正規分布」に近似できることがわかっています。下に示したグラフは試行回数80回の場合を「正規分布」で近似したものです。二項分布を正規分布で近似することで、様々な統計的計算が可能になります。

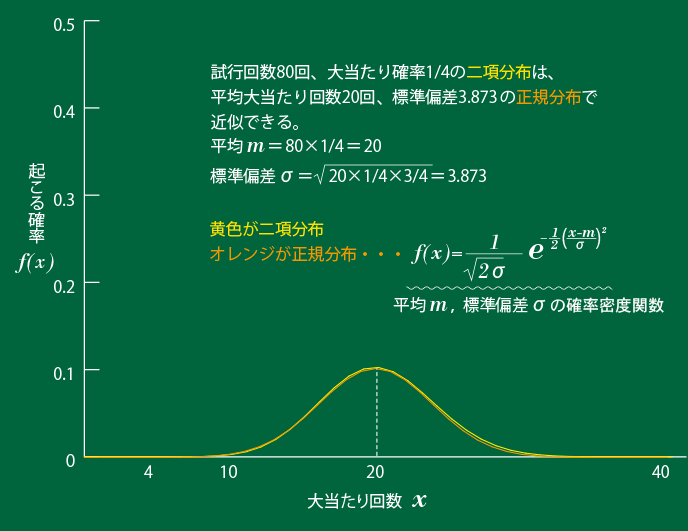
やたら複雑な式が出てきましたが、覚える必要はありません。平均と標準偏差が判っていれば具体的な式で表すことができ、グラフにもできるということを知っていれば充分です。さらにこの式を必要な範囲で積分すれば、例えば「80回の試行で大当たりが18回から22回起こる確率」などを計算することができます。

確率密度関数の値も積分した結果の確率もエクセルなどで簡単に求めることができます。（このページの最後でエクセルのデータをダウンロードできます）

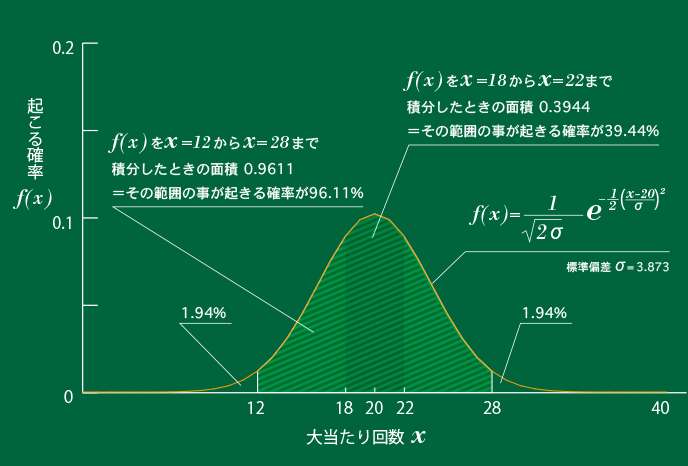
５．確率の収束とは

上の図から、次のようなことが読みとれます。
確率1/4のくじ引きを80回（１回100円としてみましょう）行うと、

• 約40％の確率で18回〜22回の当たりが見込める。
• 約96％の確率で12回〜28回の当たりが見込める。
• 当せん金額が667円（12回で8000円）以上なら80回やればほぼ勝てる。
  →80回やったとき収支がマイナスになる確率は２％以下。
• 当せん金額が285円（28回で8000円）以下なら80回やれば「胴元」はほぼ勝てる。
  →80回やったとき「胴元」の収支がマイナスになる確率は２％以下。

「確率が収束する」とは上の例で言えばこういうことです。

1/4の確率なら約80回試行すれば96％の確度で1/2.9〜1/6.7内に落ち着く
（28/80≒1/2.9、12/80≒1/6.7）

間違っても、「最初の40回で15回も当たりを引いたら次の40回では5回くらいしか当たらない」というような事ではありません。
また、当たりの確率さえ判っていれば、試行回数、確度、範囲（例で言えば80回、96％、1/2.9〜1/6.7）の３つの内２つを決めれば残る１つを計算できることになります。
例えば1/315のパチンコでは、

1. 95％の確度で理論上の確率との誤差を１％以内にするには何回転回せば良いか
2. ４万回転させた場合、90％の確度なら確率はどんな範囲に収まるか

などが計算できるというわけです。

６．パチンコの場合

やっと本題です（笑）　上のＡとＢを計算してみましょう。

Ａ　95％の確度で理論上の確率との誤差を１％以内にするには何回転回せば良いか

確率の分母（この場合315）をｋ、理論上の確率との誤差をｒ（この場合0.01）と書くと、求める回数ｎは、

ｎ＝1.96²×(k-1)÷r²
　＝1.96²×314÷0.01²
　＝12,062,624

1.96は確度95％から決まる数値で、確度90％ならここを1.64にします。このことを含めてもう少し詳しい説明はこちら

何と1200万回転必要となります。一人でやるとなると20年近くかかる(T-T)
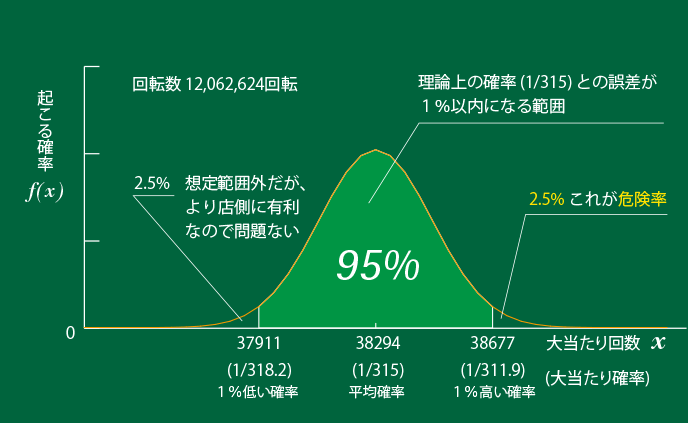
しかし200台あって稼働率60％もあれば１ヶ月で達成できます。理論上の確率との誤差１％以内ということは1/311.9〜1/318.2の範囲ですから、店としては平均して1/311.9で大当たりが出てしまっても利益が出るように釘を調整しておけば、月単位の収支がマイナスになる確率（危険率）は2.5％ということになります。10年間（120ヶ月）でたった三月です。こうして店の経営は安定するわけです。
（厳密には確率変動か否かのバラツキや打つ側の投資額のバラツキもあるため、店側の危険率はもう少し上がります。が、その分釘を調整すればいいだけです）

注：確度95％なので範囲外の結果が出る確率が５％。良い方に外れる場合と悪い方に外れる場合があるので半分の2.5％が危険率ということになります（下図参照）。

次にＢを求めてみましょう。

Ｂ　４万回転させた場合、90％の確度なら確率はどんな範囲に収まるか

まずは理論上の確率との誤差何％の範囲に収まるのかを計算します。Ａと同様に確率の分母（この場合315）をｋ、試行回数（この場合４万回）をｎ、求める誤差をｒとすると、

ｒ＝1.64×(k-1)^1/2÷ｎ^1/2
　＝1.64×314^1/2÷40000^1/2
　≒0.1453
（ｘ^1/2とはルートｘのことです）

誤差が0.1453と求められたので、求める確率の範囲は、

315÷(1+0.1453)＝275.0
315÷(1-0.1453)＝368.6
∴1/275.0〜1/368.6

これが４万回転のときの収束範囲です。４万回転というのはいわゆるパチプロの方なら１ヶ月で消化できる回転数です。これだけやれば悪くても1/368.6くらいは見込めるというわけです。平均1/368.6でも収支プラマイゼロになるような台を選んで打てば、月単位でマイナスになる確率が５％（確度90％なので危険率は10％の半分で５％）。５年間（60ヶ月）で三月です。
（これも店側の危険率同様、厳密にはもう少し上がります）
ここで回転数が１万回転だったとしましょう（熱心な週末パチンカークラス）。同様に計算すると、収束範囲は

1/243.9〜1/444.6

１万回転程度ではこのように収束範囲が広すぎて、収支は安定しないでしょう。１万回転で４万回転と同じ様な収束範囲にするには確度を59％まで下げなければならず、その結果危険率は20.5％（(100-59)/2）となり、パチプロのように台を選べたとしても５ヶ月に一度は収支マイナスになります。
（これも同様に危険率はもう少し上がります）

この「１万回転より４万回転させた方が収支が安定する」ということこそ「確率が収束する」ということなのです。

７．おまけ

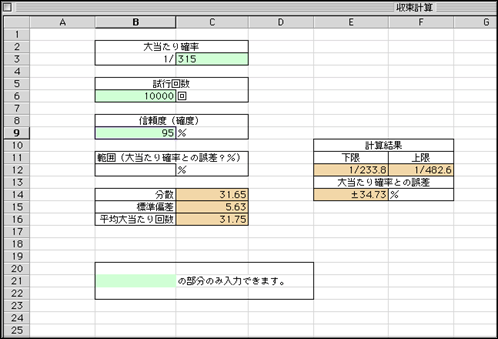
上の方でエクセルで簡単に計算できると書いたので、エクセルのデータをダウンロードできるようにしました。
ご自分でいろいろと数値を入れてみて下さい。上で計算した値と微妙に異なる結果が出ますが、それは有効桁数の取り方が違うだけですので大勢に影響ありません。

エクセルデータをダウンロードする
windows ieの方・・・右クリック→対象をファイルに保存
macintoshの方・・・普通にクリック
（うまくいかない時は、メール下さい。フォローします）