第35回 期待値の計算 | シンフォギア3
個別機種の期待値計算が続いていますが、シンフォギア3のスペックがおおよそ判明したのでやってみました。
振り分けが細かかったりRushが2種類あったりと複雑なのでシミュレータを作って検証もしました。
しかしスペックなどの理解不足があれば計算もシミュも同じミスを含んでいるかもしれません。もし間違いを見つけたらコメントいただけると大変嬉しいです。
公式ページではまだ詳細スペックは出ていません。詳細が出たら修正します。
0.シンフォギア3の期待出玉
結果を先に書きます。
【表1】初当たりごとの期待出玉など
| 平均総ラウンド数(注1) | 21.90 ラウンド |
| 期待出玉(注2) | 3,065.53 玉 |
| 等価ボーダー | 16.29 rpk |
(注1)上下のアタッカーで1R出玉が異なるので、上アタッカー1R→0.4Rとして計算
(注2)右打ち中の増減なし、アタッカーこぼれ・オーバー入賞なしの出玉
初当たり100万回のシミュレーションで、上位Rush(絶唱FEVER)に突入したケースとそうでないケースの違いは以下のとおりです。
【表2】上位Rush(絶唱FEVER)の威力
| 件数 | 平均獲得ラウンド | |
| 絶唱FEVER突入 | 66,669 | 82.47R |
| 絶唱FEVER非突入 | 933,331 | 17.58R |
| 全体 | 1,000,000 | 21.91R |
初当たり100回中6〜7回の割合で上位Rush(絶唱FEVER)に突入し、突入しない場合の5倍程度の期待出玉があります。
1.シンフォギア3のスペック
【表3】シンフォギア3のスペック
| 大当たり確率 | 1/199.8 | |
| 右打ち中確率 | 1/7.8 | |
| c時短 | 右打ち中の残保留のみ1/409.6で抽選。 当選するとSC(時短250+4回)へ。 | |
| 時短回数 | 1+4回 or 7+4回 or 250+4回 | |
| アタッカー賞球 | 上:7カウント9個 | |
| 下:10カウント15個 | ||
| 振り分け (ヘソ特図1) | 6R上 最終決戦(時短1+4回) | 74.0% |
| 6R上 SC(時短7+4回) | 25.5% | |
| 10R SC(時短250+4回) | 0.5% | |
| 振り分け(最終決戦・SC) | ||
| 右特図2 (1/199.8) | 6R上 SC(時短7+4回) | 50.0% |
| 10R 絶唱FEVER | 50.0% | |
| 右小当たり (1/7.8) | 4R(下1上3) SC(時短7+4回) | 43.4% |
| 4R(下1上3) SC(時短250+4回) | 4.5% | |
| 6R SC(時短7+4回) | 0.9% | |
| 6R SC(時短250+4回) | 0.1% | |
| 7R SC(時短7+4回) | 0.9% | |
| 7R SC(時短250+4回) | 0.1% | |
| 10R SC(時短7+4回) | 45.0% | |
| 10R SC(時短250+4回) | 4.5% | |
| 10R 絶唱FEVER | 0.6% | |
| 振り分け(絶唱FEVER) | ||
| 右特図2 (1/199.8) | 6R上 SC(時短7+4回) | 50.0% |
| 10R 絶唱FEVER | 50.0% | |
| 右小当たり(1/7.8) | 4R(下1上3) SC(時短7+4回) | 25.0% |
| 4R(下1上3) SC(時短250+4回) | 4.5% | |
| 6R SC(時短250+4回) | 0.1% | |
| 7R SC(時短250+4回) | 0.1% | |
| 4R(下1上3) 絶唱FEVER | 18.4% | |
| 6R 絶唱FEVER | 0.9% | |
| 7R 絶唱FEVER | 0.9% | |
| 10R 絶唱FEVER | 50.1% | |
右打ち中は小当たり以外にいわゆる199直(特図当り)もあり、1/7.8は両者の合算確率です。 そのため振り分けも特図当たり・小当たりの出現割合に応じて合算しておきます。
【表4】シンフォギア3の振り分け(199直・小当たり合算)
| 最終決戦 ・SC | 4R(下1上3)SC(時短7+4回) | 約41.7% | 約88.6% |
| 6R上 SC(時短7+4回) | 約2.0% | ||
| 6R SC(時短7+4回) | 約0.9% | ||
| 7R SC(時短7+4回) | 約0.9% | ||
| 10R SC(時短7+4回) | 約43.2% | ||
| 4R(下1上3)SC(時短250+4回) | 約4.3% | 約8.8% | |
| 6R SC(時短250+4回) | 約0.1% | ||
| 7R SC(時短250+4回) | 約0.1% | ||
| 10R SC(時短250+4回) | 約4.3% | ||
| 10R 絶唱FEVER | 約2.5% | 約2.5% | |
| 絶唱 FEVER | 4R(下1上3) SC(時短7+4回) | 約24.0% | 約26.0% |
| 6R上 SC(時短7+4回) | 約2.0% | ||
| 4R(下1上3) SC(時短250+4回) | 約4.3% | 約4.5% | |
| 6R SC(時短250+4回) | 約0.1% | ||
| 7R SC(時短250+4回) | 約0.1% | ||
| 4R(下1上3) 絶唱FEVER | 約17.7% | 約69.5% | |
| 6R 絶唱FEVER | 約0.9% | ||
| 7R 絶唱FEVER | 約0.9% | ||
| 10R 絶唱FEVER | 約50.1% |
獲得ラウンド数の計算では以下のとおり補正します。
・6R上 → 2.4R
・4R(下1上3)→ 2.2R
2.遷移図
下位Rush(SC)と上位Rush(絶唱FEVER)を行ったり来たりします。
【図1】シンフォギア3 の状態遷移図
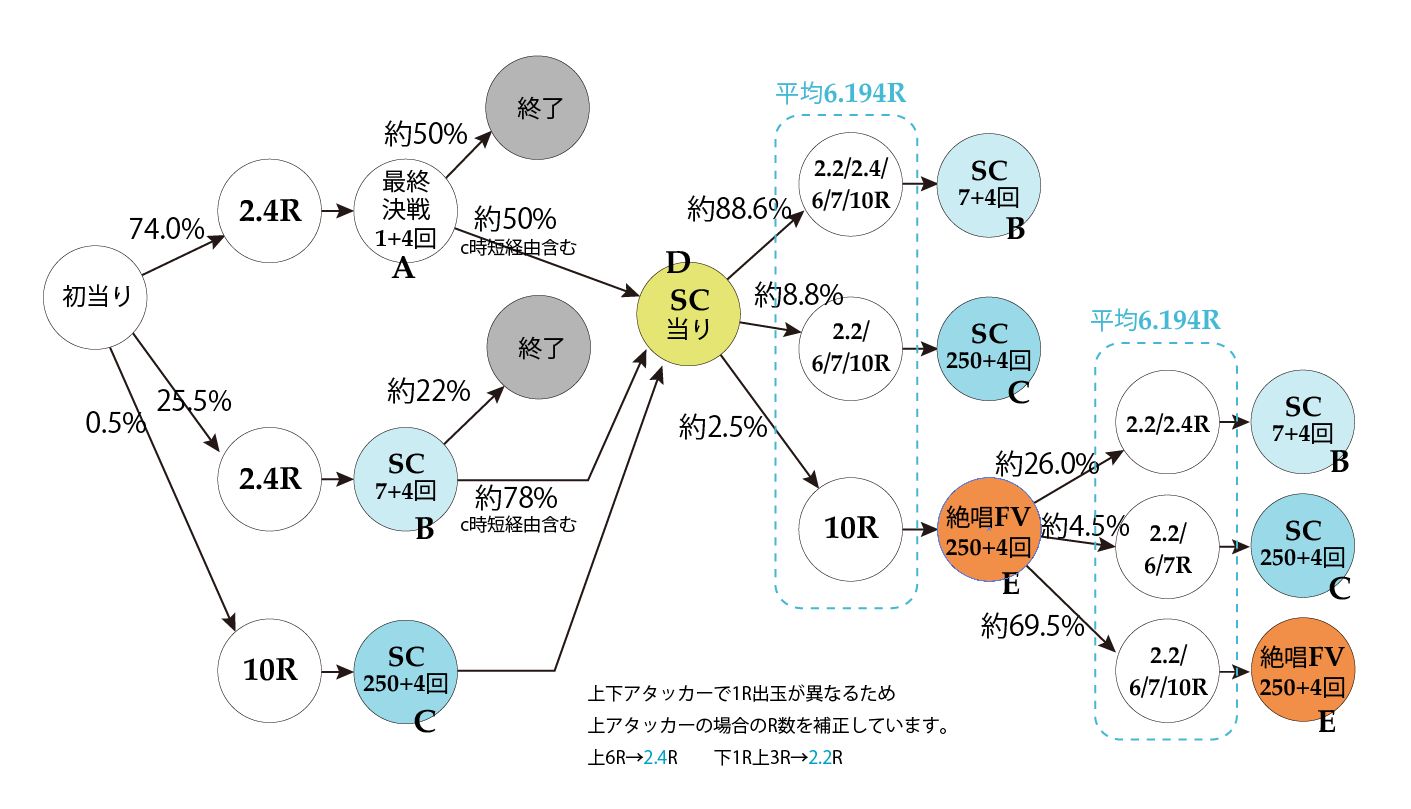
まずは図中の A〜 E それぞれの状態になったときの「それ以降」の期待獲得ラウンド数を計算します。
そのあと初当たり時の振り分けに従って合算すれば、初当たり1回の期待獲得ラウンド数が求まります。
3.準備
【表5】各種計算
| c時短考慮の右打ち中確率(注1) | \(\dfrac{1}{7.8}+\dfrac{1}{409.6}=\dfrac{1}{7.654}\) | 0.1306 |
| 最終決戦(時短1+4回)突破率 | \(1-(1-\dfrac{1}{7.8})^{1} \times(1-\dfrac{1}{7.654})^{4}\) | 0.5020 |
| 時短7+4回突破率 | \(1-(1-\dfrac{1}{7.8})^{7} \times(1-\dfrac{1}{7.654})^{4}\) | 0.7814 |
| 時短250+4回突破率 | \(1-(1-\dfrac{1}{7.8})^{250} \times(1-\dfrac{1}{7.654})^{4}\) | 1.0000 (注2) |
| SC平均ラウンド | \(2.2R\times0.417+…+ 10R\times0.025\) | 6.194R |
| 絶唱FV平均ラウンド | \(2.2R\times0.24+…+ 10R\times0.501\) | 6.194R |
| 1R出玉(注3) | \(10\times(15-1)\) | 140玉 |
(注1)c時短の抽選仕様は不明ですが、図2のように想定しています。
(注2)厳密には100%ではありませんが以降の計算では100%としています。ちなみにExcelでは0.9999999999999990で9が15個続きます。一京回に1回スルーする確率です。
(注3)上述したとおり上アタッカー分の補正をすることで1R=140玉に統一します。
【図2】想定した当り判定カウンターの模式図
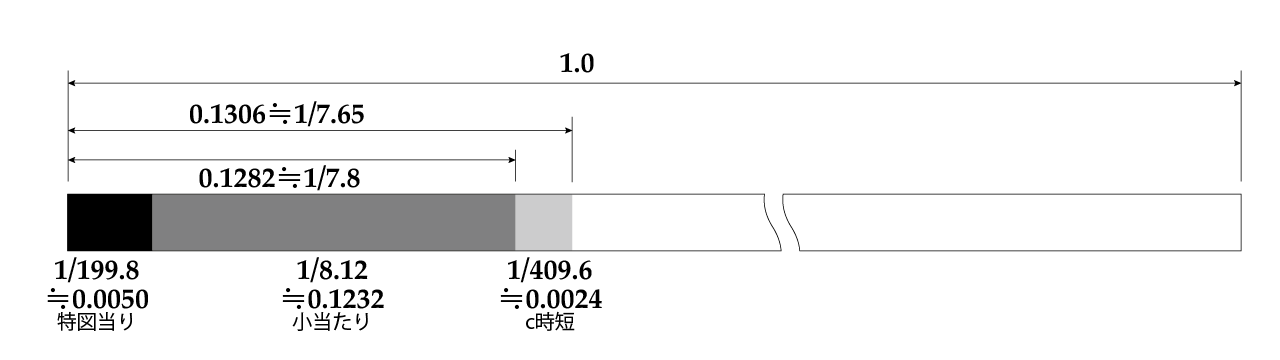
図中小当たりの1/8.12は公式ページの1/199.8と1/7.8とから逆算した値で、公式ページが「約」1/7.8にと書かれていることもあり、正確にはわかりません。また1/199.8は200/39961(=1/199.805)の可能性が高いですが公式発表どおり1/199.8で計算しています。
4.初当たり時期待総ラウンド数
「初当たり時期待総ラウンド数 \(E_R\)」を計算します。
上述したとおり、図中の A〜E それぞれの状態になったときのそれ以降の期待獲得ラウンド数を計算します。
それぞれの「状態」の内容を確認しておきましょう(図中の言葉で書いています)。
A 最終決戦 時短1+4回 →(終了 or SC当り)
B SC 時短7+4回 →(終了 or SC当り)
C SC 時短250+4回 →(SC当り)
D SC当り →(平均6.194R獲得してSC時短7+4回 or SC時短250+4回 or 絶唱FV)
E 絶唱FV →(平均6.194R獲得してSC時短7+4回 or SC時短250+4回 or 絶唱FV)
【図1再掲】シンフォギア3 の状態遷移図

Aが起きた時の「以降の」平均獲得ラウンド数を\( A\)と書くことにします。
\[
\begin{align}
A =& 0.502\times D + (1-0.502) \times 0\\
\end{align}
\]
前半は1+4回時短の突破率0.502と突破した時(=状態D)の平均獲得ラウンド数\( D\)をかけています。
後半の(1-0.502)は突破できなかった時ですが獲得ラウンドがありませんのでゼロをかけています。
そのような計算を表にまとめると次のようになります。
【表6】状態別平均獲得ラウンド数の計算
| 起こる確率 | ラウンド数 | |||
| A | 0.502 | \( D\) | \(0.502 \times D\) | |
| 1-0.502 | 0 | |||
| B | 0.7814 | \( D\) | \(0.7814 \times D\) | |
| 1-0.7814 | 0 | |||
| C | 1.0 | \( D\) | \( D\) | |
| D | 0.886 | \(○R + B\) | \(=6.194R \) \(+ 0.886 \times B\) \( + 0.088 \times C \) \( + 0.025 \times E \) | \(=6.194R \) \(+ 0.886 \times (0.7814\times D) \) \(+ 0.088 \times D \) \(+ 0.025 \times E \) \(=6.194R + 0.781 \times D+0.025 \times E\) |
| 0.088 | \(△R + C\) | |||
| 0.025 | \(□R + E\) | |||
| E | 0.26 | \(○R + B\) | \(=6.194R \) \(+ 0.26 \times B\) \( + 0.045 \times C \) \( + 0.695 \times E \) | \(=6.194R \) \(+ 0.26 \times (0.7814\times D) \) \(+ 0.045 \times D \) \(+ 0.695 \times E \) \(=6.194R + 0.248 \times D+0.695 \times E\) |
| 0.045 | \(△R + C\) | |||
| 0.695 | \(□R + E\) | |||
表中DとEのラウンド数の欄が○、△、□で書かれていますが、表4の振り分け率で計算を進めても結局平均ラウンド6.194が出てくるだけなので省略しています。
Dの最後の式は、 \[ \begin{align} D =& 6.194R + 0.781 \times D + 0.025 \times E \\ \end{align} \] となっています。 \(0.781 \times D\)を左辺に移項して \[ \begin{align} (1-0.781)\times D =& 6.194R + 0.025 \times E \\ D =& \dfrac{6.194}{0.219}R + \dfrac{0.025}{0.219}\times E \\\\ D =& 28.28R + 0.115\times E \\\\ \end{align} \] 一方Eの最後の式は、 \[ \begin{align} E =& 6.194R + 0.248 \times D + 0.695 \times E \\ \end{align} \] となっています。 \(0.695 \times E\)を左辺に移項して \[ \begin{align} (1-0.695)\times E =& 6.194R + 0.248 \times D \\ E =& \dfrac{6.194}{0.305}R + \dfrac{0.248}{0.305}\times D \\\\ E =& 20.31R + 0.814\times D \\\\ \end{align} \] Dの式を使って \[ \begin{align} E =& 20.31R + 0.814\times (28.28R + 0.115\times E) \\\\ =& 43.32R + 0.0934\times E \\\\ \end{align} \] \(0.0934 \times E\)を左辺に移項して整理すれば \[ \begin{align} (1-0.0934) \times E =& 43.32R \\ \textcolor{orange}{E} = & \textcolor{orange}{47.82}R \end{align} \] よって \[ \begin{align} \textcolor{orange}{D} = & 28.28R+0.115 \times E&= \textcolor{orange}{33.80}R\\ \textcolor{orange}{C} = & D &= \textcolor{orange}{33.80}R\\ \textcolor{orange}{B} = & 0.7814\times D &= \textcolor{orange}{26.41}R\\ \textcolor{orange}{A} = & 0.5020\times D &= \textcolor{orange}{16.97}R\\ \end{align} \]
これでそれぞれの「状態」以降の期待獲得ラウンド数が求まりました。
この結果のEは「絶唱FEVER」突入以降の平均獲得ラウンド数です。突入以降の平均出玉6,694玉となります。
初当たり時は74%で2.4R+A、25.5%で2.4R+B、0.5%で10R+Cの振り分けです。
よって初当たり時期待総ラウンド数 \(E_R\) は
\[
\begin{align}
\textcolor{orange}{E_R}=& 0.74 \times( 2.4R + A)+ 0.255 \times( 2.4R + B)+ 0.005 \times( 10R + C) \\
=& 0.74 \times 19.37R+ 0.255 \times 28.81R + 0.005 \times 43.80R \\
=& \textcolor{orange}{21.90}R\\
\end{align}
\]
で、冒頭の表のとおり、1ラウンド140玉とすれば期待出玉は 3,065玉、等価ボーダーは16.29rpkとなります。
シミュレーション結果は次のとおり。
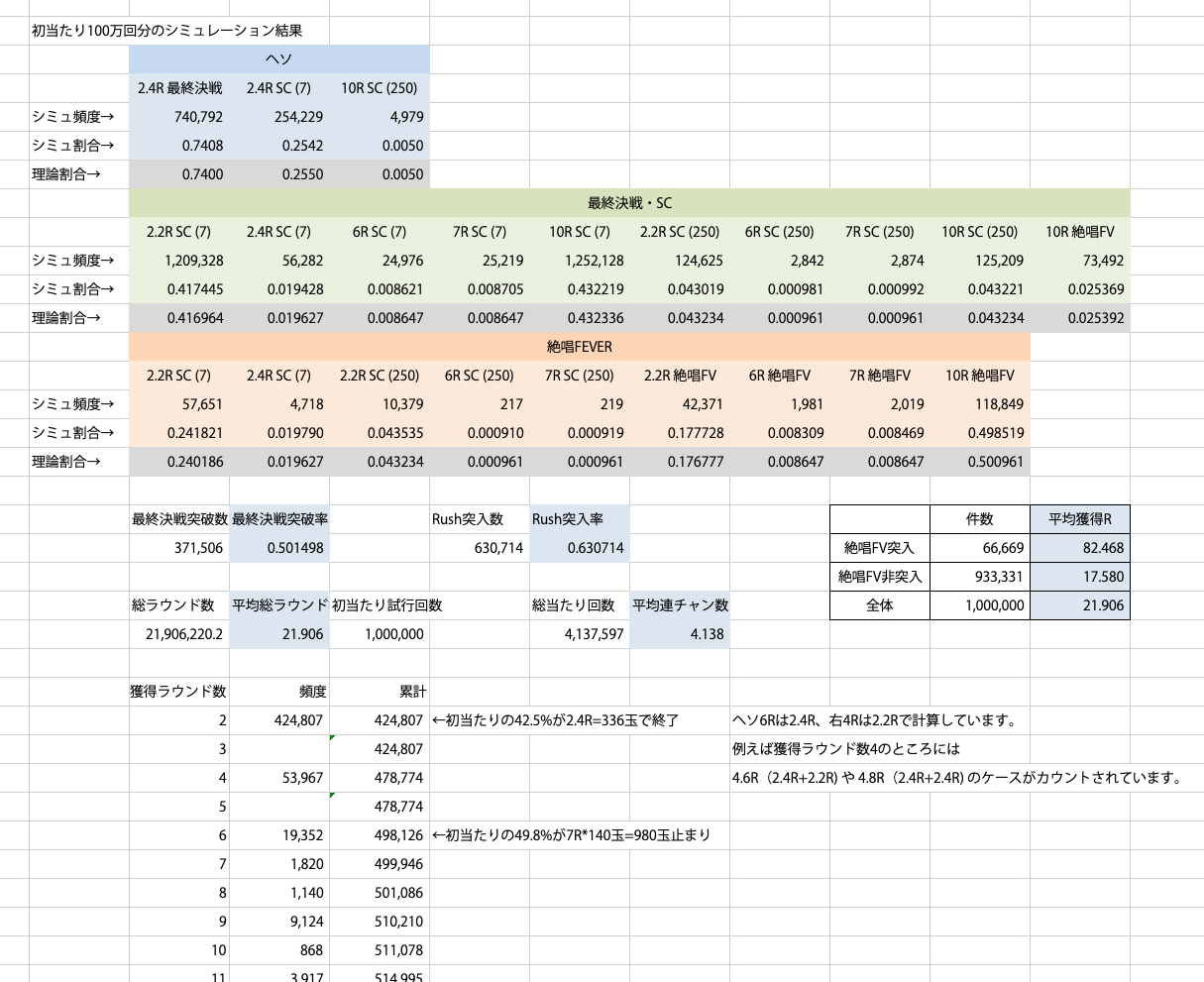
5.補足
(以下、ヴヴヴ2の時と同じ内容ですが、再掲しておきます)
あまり見慣れない計算方法と思われる方もいるかもしれません。
参考までに普通のST機の「ST突入」以降の期待ラウンド数の計算を、よく知られている方法と今回の方法とで比較してみました。ちゃんと同じ結果になります。
\(\dfrac{1}{1-r}\)は突入時を含む継続回数なので1を引くことを忘れずに。
【図2】通常の計算方法との比較
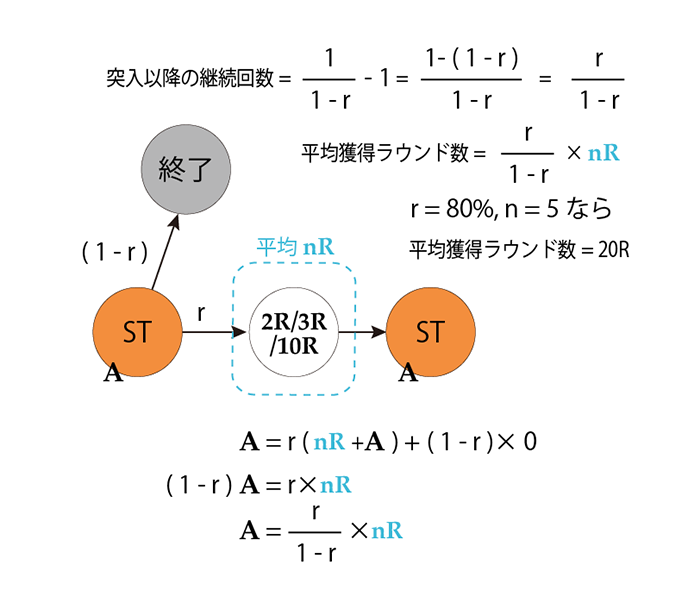
第37回 期待値の計算 | P地獄少女覚醒3000
第36回 期待値の計算 | P牙狼11 冴島大河 XX
第34回 期待値の計算 | ヴヴヴ2 199ver.
第33回 期待値の計算 | EVA15 未来への咆哮
第32回 期待値の計算 | Pめぞん一刻5
第31回 休憩 | 回りムラのシミュレーション
第30回 期待値の計算 | PFアイドルマスター(3)
第29回 期待値の計算 | PFアイドルマスター(2)
第28回 期待値の計算 | PFアイドルマスター(1)
第27回 期待値の計算 | シンフォギア2
第26回 期待値の計算 | ボーダー理論の解説(1)
第23回 逆正弦定理 〜ボーダー理論は否定される?
第22回 ボーダー理論のビジュアル化
第21回 確率はホントに収束するのか
第17回 パチンコはどれくらいハマるのか
