第9回 休憩
今回はネタ切れなので、短い話題を2つほど紹介してお茶を濁すことにします^^;)
1.なぜ当選確率63%か
最初は第3回で示した「試行回数と当選確率」の関係で、200分の1の確率のゲームを200回行ったときの当選確率が100%でなく63%程度であることについてです。いわゆるパチンコでいうところの「1倍ハマリを喰らわない確率」ですね。
200回試行しているのに、なぜ100%にならないのか?
答えは非常にシンプルです。下の図を見て下さい。正確に200回に1回当たるとすると、どの連続する200回を取りあげても、常に1回当たりが入っています。しかし1回以上当たることはありません。
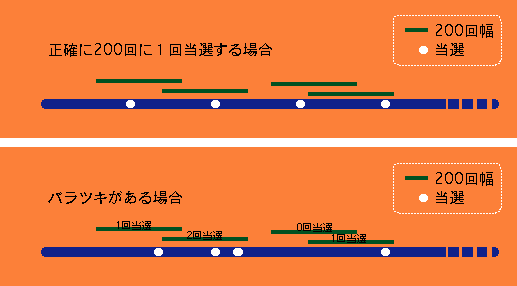
一方、当たりにバラツキがある場合は、連続する200回の取り方によって2回当たりが入っていたり、1回も入っていなかったりします。
この2つの違いは、宝くじの末等当選における「連番」買いと「バラバラ」買いの違いに似ています(厳密にはもちろん違いますが...)。
「バラバラ」買いとは、いわゆる「バラ」ではなく、末尾の数字もバラつくように買う方法です。宝くじの末等は10枚に1枚の割合で入っていて、全体はこれより多くも少なくもありません。
「連番」で10枚買う場合、どの数字からの10枚でも必ず1枚の当たりがあり、「バラバラ」で10枚買う場合は2枚当たることもあれば、1枚も当たらないこともあるわけです。
つまりはバラツキのなせる技なのです。200回試行したときのn回当たる確率をグラフにしてみました。
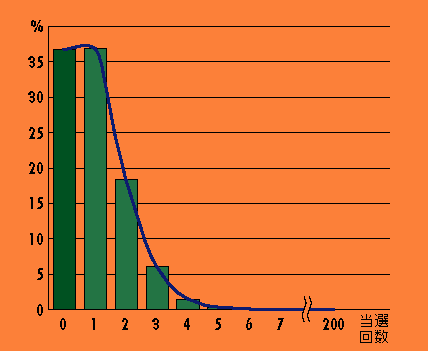
このグラフの色の薄い部分が約63%なのです。
2.無限ということ
次は無限について考えてみます。
確率をはじめ、数学を論ずる上で、永遠とか無限という概念は非常に重要です。
この講座でも何度となく、「永遠に試行する」場合と現実世界の違いを書いてきたつもりです。しかし、普通に生活しているとなかなか「無限」の持つ不思議な側面をみることができません。
数学では物事を厳密に突き詰めるため、こうした「無限」の不思議に出会えます。
では問題です。
- 偶数と奇数はどちらが多いか?
- 自然数と偶数はどちらが多いか?
- 2の倍数と8の倍数はどちらが多いか?
- 4cmの線分上の点と8cmの線分上の点はどちらが多いか?
*自然数というのは1以上の整数(1,2,3,4,....)のことです。
答えはすべて「同じ」です。下の表を見て下さい。
| 自然数 | 偶数 | 奇数 | 8の倍数 |
| 1 | 2 | 1 | 8 |
| 2 | 4 | 3 | 16 |
| 3 | 6 | 5 | 24 |
| 4 | 8 | 7 | 32 |
| 5 | 10 | 9 | 40 |
| 6 | 12 | 11 | 48 |
| ・ ・ ・ | ・ ・ ・ | ・ ・ ・ | ・ ・ ・ |
| n | 2n | 2n-1 | 8n |
| ・ ・ ・ | ・ ・ ・ | ・ ・ ・ | ・ ・ ・ |
偶数も奇数も8の倍数も自然数と1対1に対応しています。
例えば自然数と偶数で上の表のようなペアを作ってみると、どちらのグループにも余りも不足もないことがおわかりいただけると思います。
4も同じです。図を見て下さい。
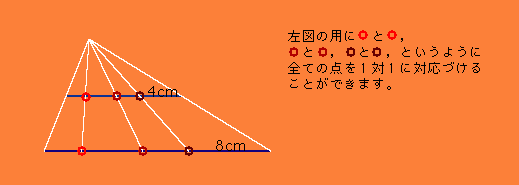
集合の要素が有限の場合、1以外は「同じ個数」ではありません。
しかし集合の要素が無限にある場合は、番号が付けられる(可付番集合=自然数と1対1対応可能)ならどちらが多いとも少ないとも言えません。
不思議ですね〜。集合論って地味だけど結構面白いんですよ。
では問題をもう2つ。

どちらも徐々に小さくなっていく分数の無限和です(無限級数といいます)。
無限に足すのだから、無限? 答えは次のとおりです。
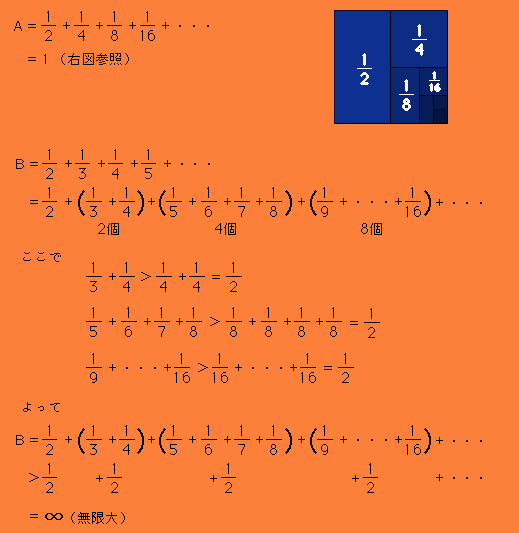
いかがでしたか。
一方は有限の答えがあり(収束するといいます)、一方は無限(発散するといいます)です。不思議ですね〜。
確率を用いるギャンブルの場合、その戦略において「無限」が絡むと気をつけなければなりません。
「無限に続ければ...」という記述は攻略本などでよく見かけますが、現実は無限に続けることは不可能ですし、無限と有限では世界が全く違うのです。今回の内容を「無限」に関する誤解の解消に役立てていただければうれしいのですが...
さて、これで第9回の内容は終わりです。
次回はちゃんとする予定です...
第36回 期待値の計算 | P牙狼11 冴島大河 XX
第35回 期待値の計算 | シンフォギア3
第34回 期待値の計算 | ヴヴヴ2 199ver.
第33回 期待値の計算 | EVA15 未来への咆哮
第32回 期待値の計算 | Pめぞん一刻5
第31回 休憩 | 回りムラのシミュレーション
第30回 期待値の計算 | PFアイドルマスター(3)
第29回 期待値の計算 | PFアイドルマスター(2)
第28回 期待値の計算 | PFアイドルマスター(1)
第27回 期待値の計算 | シンフォギア2
第26回 期待値の計算 | ボーダー理論の解説(1)
第25回 ナンバーズ3 高配当を狙え part2 | 日付に読めない数字
第23回 逆正弦定理 〜ボーダー理論は否定される?
第22回 ボーダー理論のビジュアル化
第21回 確率はホントに収束するのか
第17回 パチンコはどれくらいハマるのか
第02回 ナンバーズの攻め方「不人気ナンバーを狙え!」
