第22回　ボーダー理論のビジュアル化　〜収支は収束しない？〜

０．動画で説明

ボーダー理論で勝てる仕組みをアニメーションで説明してみました。
文章なんて読んでらんねー！って方は↓をどうぞ♪

１．はじめに

確率が収束するとはどういうことなのか…
「第21回 確率はホントに収束するのか」で説明しました。
パチンコにおいては、確率が収束することで店もパチプロも収支が安定するという説明もしました。

しかし、確率が収束してもトータル収支は収束しないということをよく聞きます。
一体どういうことなのでしょうか。

トータル収支が収束しないなら店もパチプロも安定した収支を得られないのでしょうか？
結論を先に書きますが、

トータル収支（累積収支）は収束しません
しかし店もパチプロも安定した収支を得られます

ますますわからなくなりますね（笑）

今回はボーダー理論で勝つとはどういうことなのか、「見てわかるボーダー理論」を目標に書いてみます。

２．累積収支が収束しないわけ

そのわけはとてもシンプルです。

「初当たり回数　÷　通常回転数」は比率（平均値）です。
一方で累積収支とは積算値（総和）です。

積算値と平均値（比率）は性質のまったく違う「量」です。

これは「試行回数が足りない」とか「有限回だから」というハナシではなく、そもそも、

比率は収束するけれど累積は収束しない

ということなのです。

３．収支はどんな挙動をするか

ここまでわかると平均収支は？と考えたくなりますよね。
まずは次のグラフを見てください。

【図１】累積収支の推移（ちょうどボーダーで300日）

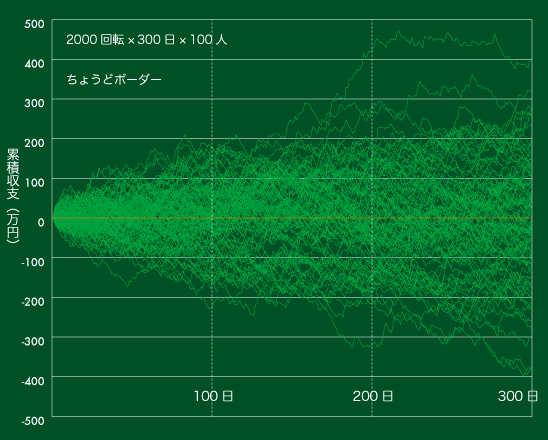
これは初代GARO「牙狼XX」を次の条件でシミュレーションしたものです。

冒頭で結論を示したとおり、累積収支は収束せずどんどん広がっていきます。300日後には一番勝った人と一番負けた人の収支の差は800万にもなっています。
では次のグラフを見てください。

【図２】平均収支の推移（ちょうどボーダーで300日）

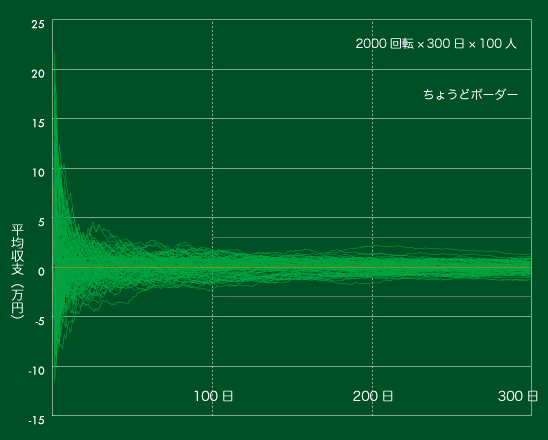
これは【図１】と同じシミュレーション結果で平均収支（平均日当）の推移を表したものです。
30日辺りでは平均収支でも10万近い差がありますが、300日後には良くて２万悪くてもマイナス２万。平均収支の差は４万程度になっています。1,000日のシミュレーションでは次のようになります。

【図３】平均収支の推移（ちょうどボーダーで1,000日）

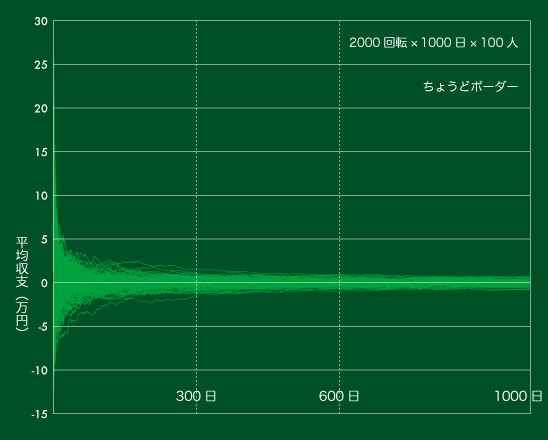
とてつもなくゆっくりではありますが、300日を超えてもまだ幅は狭まっていきます。

平均収支は収束します
期待値ゼロの勝負を延々と続ければ平均収支はゼロに限りなく近づきます

さて、ここからが重要です。

４．期待値プラスを追いかけてトータルで勝てる理由

平均収支が収束することがわかったとしても、累積収支が発散するなら「トータルで勝つ」にはどうしたら良いでしょうか？

結論から言えば、

期待値（仕事量）を積み上げてグラフを右肩上がりにする

ということになります。
次のグラフを見てください。

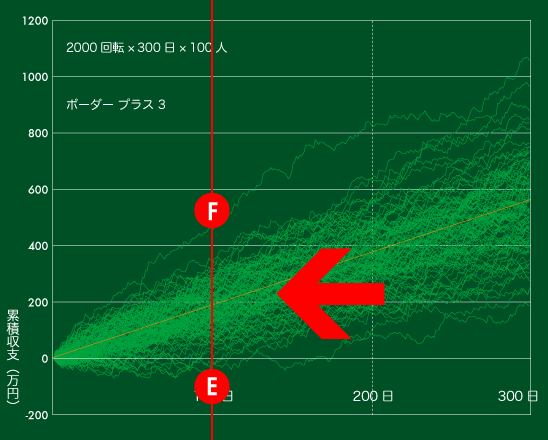
【図４】累積収支の推移（ボーダー ＋３ で300日）

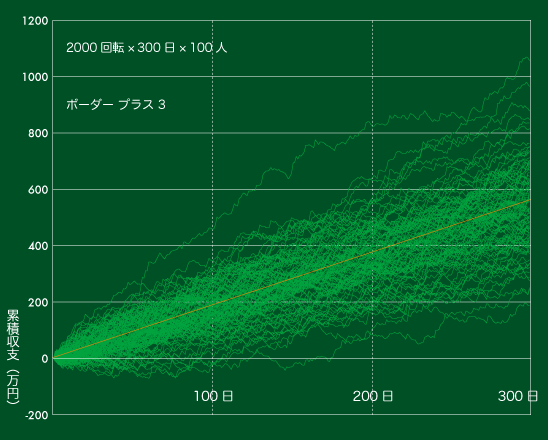
このグラフはボーダー ＋３で【図１】と同じ当たり方をしたときの累積収支の推移です。
ちょうどボーダーのケースと同様に、300日後の収支の幅は800万ありますが、すべてがプラス収支になっています。
薄いオレンジで示した直線は期待日当に日にちを乗じたもので、どの日にちで切り取ってもオレンジの線を中心に結果が分布していることがわかるかと思います。累積収支は収束しませんが、累積期待値の周囲に分布することから逃れることはできません。

期待値（仕事量）を積み上げて収支を安定させる「ボーダー理論」は、分布の中心となるライン（オレンジのライン）を右肩上がりにするということに他なりません。

現実にはオレンジのラインは直線ではなく階段状だったりします。ましてや期待値マイナスの台を長いこと打ってしまえば、累積期待値は右肩上がりにはなりません。ボーダー以下の台ばかりを打ってしまえば次のようになります。

【図５】累積収支の推移（ボーダー マイナス３ で300日）

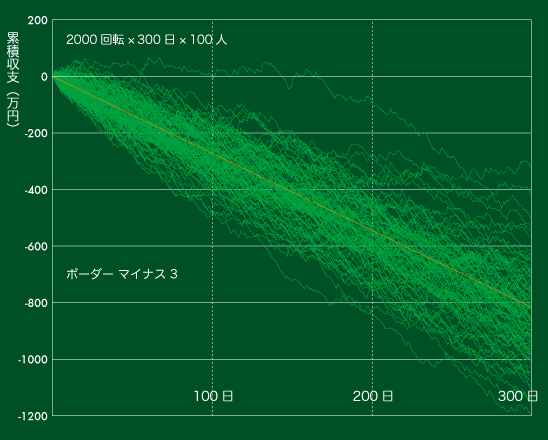
このグラフも【図１】と同じ当たり方をしていますが、収支は惨憺たるものです。多少ツイている時期があっても、累積期待値からかけ離れた収支（プラスでもマイナスでも）を維持することは不可能です。

ときどき「ボーダー理論はただの節約効果で、勝てるかどうかは運のみ」などというハナシも聞きますが、そうではないのです。長期的に見れば勝つべくして勝ち、負けるべくして負けるのです。

５．バラツキをどう捉えるか

さて、【図１】では最も負けた人でもマイナス400万ですが、実際にはもっと負ける人がいるのでは？　パチンコの抽選がホントに正しく行われているならむしろ100日間まったく当たりが引けない人もいるのでは？　という疑問はどうでしょうか。

それはもっともな疑問で、2,000回転×100日で一度も当たりを引けない可能性は否定できません。
収支が累積期待値の周囲に分布するといっても、どのくらいの範囲に散らばるのでしょうか。

パチンコの収支は大当たり回数に依存します。牙狼XXは出玉が一種類ですので、総当たり回数の分布がそのまま収支の分布になります。

近年はラウンド数の異なる何種類かの当たりがあるなど、回数だけでは測れませんが考え方は同じです。

下の図を見てください。

【図６】総当たり回数の分布（１日）

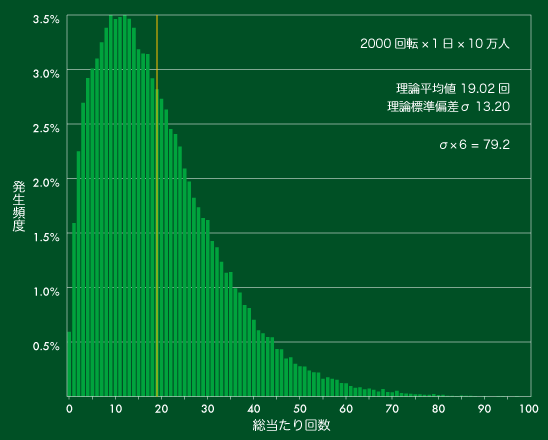
【図６】では平均は19回ほどですが、グラフのピークは左（大当たりが少ない方）に偏っています。これは2,000回転程度だと運の要素が大きく、当たりが極端に多い少数の人の結果が全体の平均値を上げていると見ることができます。
このケースでは平均より大当たり回数の少ない人（大当たりが19回以下の人）は全体の６割近くになります。

このように最も多くの人が属する部分（グラフのピーク＝最頻値）が平均とならないことは珍しくありません。

試行回数が増えれば（日にちを増やせば）グラフは少しずつ左右対称の釣り鐘型に近づいていきます。
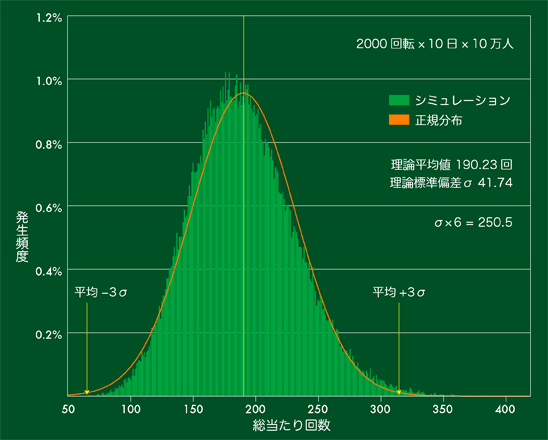
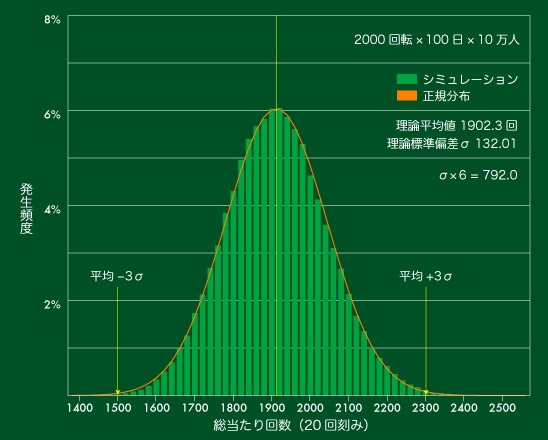
【図７】【図８】と見ていただければわかるとおり、正規分布と重なるように推移します。

【図８】でも若干左に偏っています。平均以下（1902回以下）の人は50.6％ほどです。

【図７】総当たり回数の分布（10日間）

【図８】総当たり回数の分布（100日間）

さて、総当たり回数の分布が回転数を増やせば正規分布に近づくことがわかりましたが、このバラツキ具合はどう評価すればよいでしょうか。

このような分布の特徴は「平均」と「標準偏差（σ：シグマ）」で決まります。
一般的にσの６倍の範囲にほとんどが収まることがわかっていて、正規分布の場合は平均マイナス３σ〜平均プラス３σの範囲に全体の99.74％が入ります。３σの外側が0.26％となりますが、プラス側マイナス側の合計が0.26％ですので、悪い方（当たりが少ない方）に限れば0.13％です。
シミュレーション結果もおおよそ６σの範囲であることがおわかりいただけると思います。

0.13％を多いと見るか少ないと見るかはお任せしますが、それ以上のヒキ弱を想定して「パチンコは勝てない」とお考えならそのとおりです。
しかし、ぜひ記録をつけてみてください。そのようなヒキ弱は狙ってもなかなかできないことがわかると思います。

牙狼XXで単発が９回続くのが0.19％。挑戦してみてください。

６．回転率による累積収支の違い

さて、次に累積収支の分布を回転率（千円で何回回るかというアレです）毎に見てみましょう。
先ほどの0.13％では納得いかない方もきっと納得いただけると思います。

次の３つのグラフを見てください。

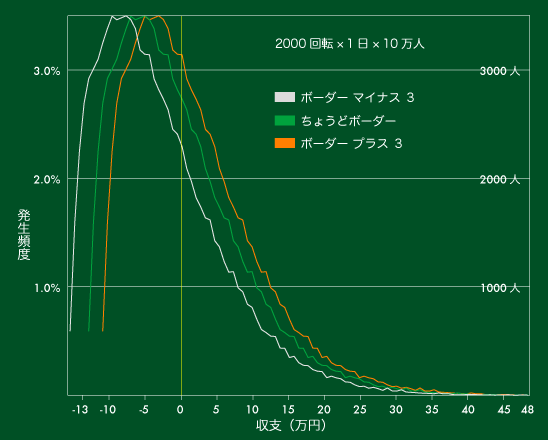
【図９】累積収支の分布（１日の収支）

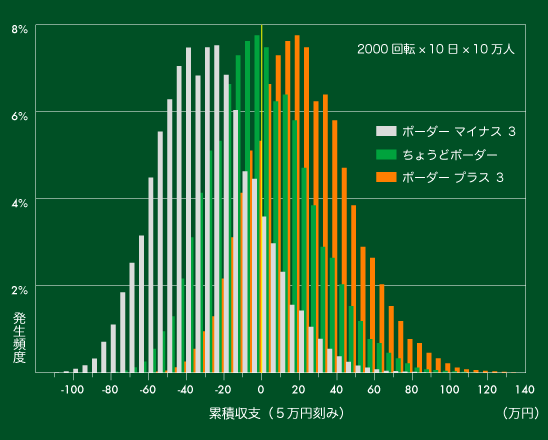
【図10】累積収支の分布（10日間の累積）

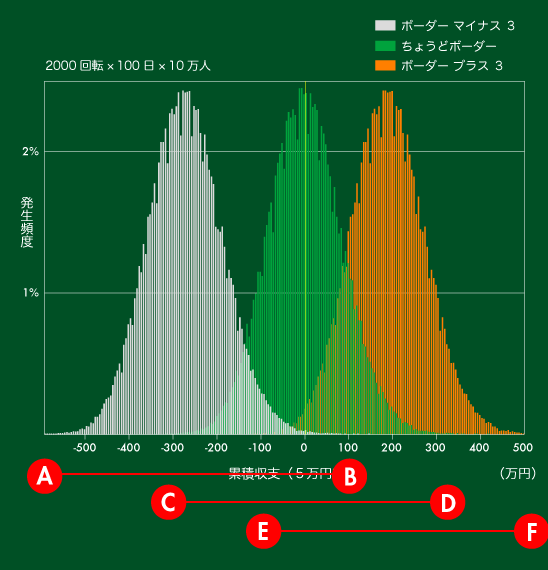
【図11】累積収支の分布（100日間の累積）

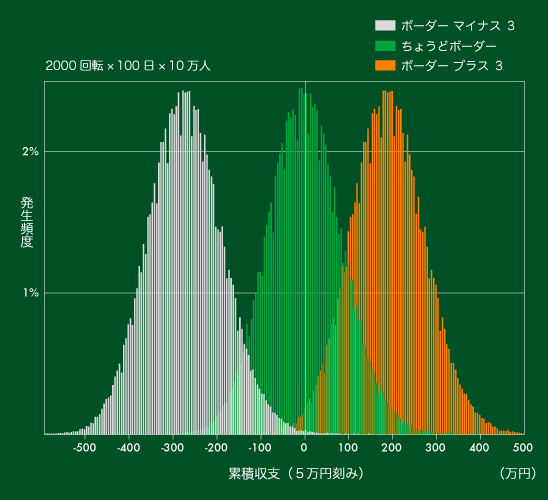
これから何が読み取れるでしょうか。

日にちを重ねる毎に白・緑・オレンジのグラフが離れていき、重なり部分が少なくなることにお気づきでしょうか。
ボーダープラス３だからといって、一日では運の要素の方が大きく、よく回る利点がほとんど効いてきません。【図９】の３色のグラフの重なり具合から明らかですね。

2,000回転程度では大きくツイていた少数の人の高額収支が平均値を高くしています。
このことからも短期間では運の要素が大きいことがわかります。

それが【図11】になると、白とオレンジはほとんど重なりがなくなります。
ボーダーマイナス３で収支をプラスにするのは至難の業ですし、ボーダー＋３で収支マイナスにするのも難しいことがわかります。

期待収支の高い勝負（ボーダーを超える勝負）を続ければ長期的には勝てるのです。

これらのグラフからわかる最も重要なことは

ボーダー＋３を打ち続けている人はボーダーマイナス３の人のように負けることはできない。

ボーダーマイナス３を打ち続けている人はボーダー＋３の人のように勝つことはできない。

ということです。

７．おまけ

【図11】と【図１】【図４】【図５】の関係にお気づきでしょうか。
【図１】【図４】【図５】を100日のところで切って下図の矢印の方向から見ると…

【図12】

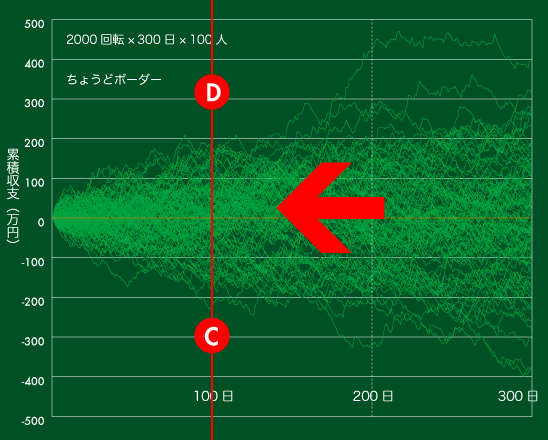
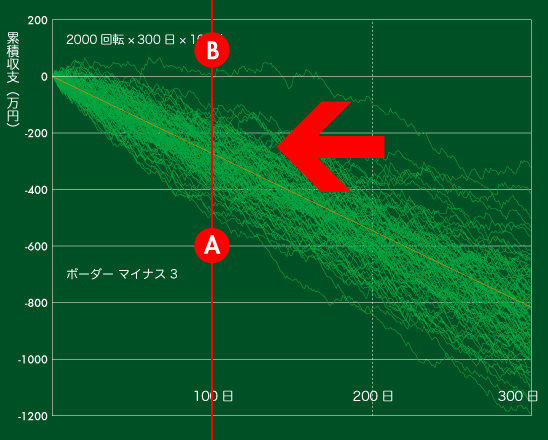
【図11】の白・緑・オレンジが200日、300日と経過するにつれて離れていくことがわかると思います。

【図13】